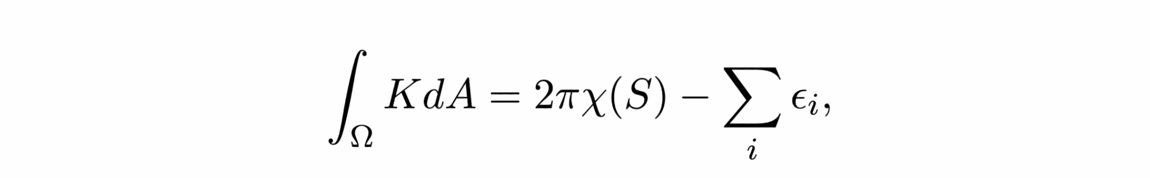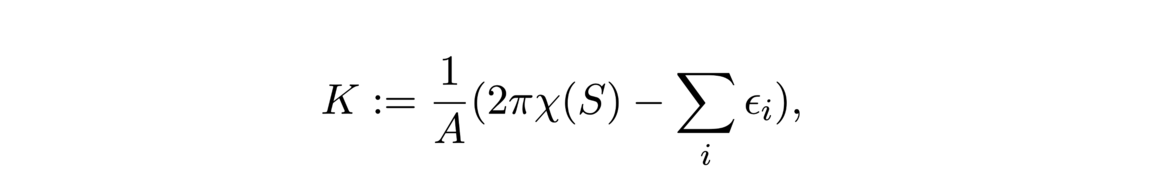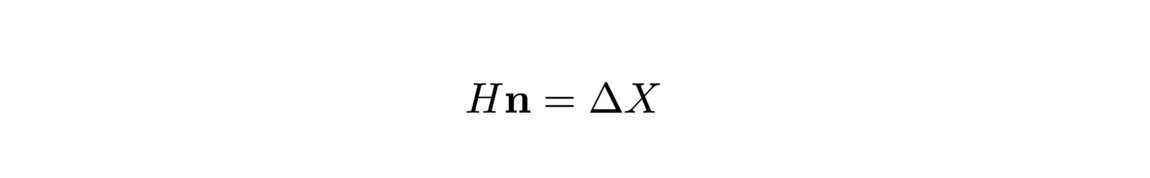The history of proof assistants began in the 1970s thanks to the work of Boyer and Moore, with a code called ACL, capable of making induction proofs with the primitive recursive arithmetic, proving simple trivial steps automatically. Later, Milner introduced the idea of tactics, which are programs safely combining primitive rules together. A change of method appeared around 1985 with Isabelle/HOL and Coq, two software based on higher-order logic (HOL) and the later precisely based on type theory. Many of these are still used nowadays. More recently, we can note in 2013 a new assistant, Lean, which uses type theory for mathematical proofs, implementing for example classical logic.
These proof assistants have already proved their worth in many situations. For Coq, let us cite as examples the proof of the 4 color theorem in 2007, the build of an optimizing C compiler, the Javacard protocols security certification, the many uses in cryptography or its use as a base language for the educational software Edukera.
Different languages
Logical proofs require a specific language to write the derivation of true properties from previous ones. For instance, the set theory approach consists in giving few axioms from which we build the mathematical objects by using logical connectives (negation, or, and, implication), and quantifiers (for all, there exists). As we build everything from basic objects, this implies many abstraction layers to hide the complexity of these constructions. Meanwhile, higher order logic and type theory, used in modern assistant proofs, rely on a lighter basis. For instance, when the inclusion relation ∈ of set theory is a primitive property that has to be proven, in higher order logic and type theory, the membership notion takes the form of what is called a typing judgment, written " a: A": the term a has type A and specific rules are associated to objects of type A.
For HOL, two logical primitive operations are used: implication and a generalized version of the "for all" quantifier, also covering propositions. Using these two it is possible to explicitly build most of the mathematical objects needed without speaking of sets.
In type theory, the types are constructed by giving explicit rules. As an example, the natural numbers N is made by giving two judgments, "0: N" and " succ : N → N", where succ is the successor function and has the “function type” from N to itself. They are the constructors of the type N. Denoting 1 := succ(0) and so on, we have built natural numbers. Indeed, we now can derive any function from natural numbers to themselves by a recursive definition: a+b becomes the b-th successor of a, and the function double: x→ 2x is defined with double(0)=0 and double(succ(n))=succ(succ(double(n))) - more generally formalized as a recursive definition on the type N. Moreover, this avoids additional axioms in the sense that every type has an internal definition.
Thus, with type theory, we can define directly many mathematical functions as programs. This is very useful to automate proofs since equality can be proven by evaluation thanks to the underlying program. For example, f(a)=b has a proof if f(a) has the value b. Nevertheless, all functions cannot be defined in this way: for instance, defining the minimum of a function from N to N recursively results into an infinite loop.
Another approach is to use functional terms to represent proofs. This is known as the Curry-Howard isomorphism: " a : A" is interpreted as "a proves A", and thus a function from A to B can be considered as a proof of B knowing A. This way, having some proposition P provable is equivalent to having the proof assistant able to compute a term of the type P, and checking a proof is the same as checking that the types are correct.
Sum of integers
Now that the main ideas of proof assistant using type theory had been given, let us show, as an example of how we can write a proof for the following identity with the Coq Software.
First, we construct the sum of the n first integers like a recursive program by using the constructor of N (nat) and the module Lia Arith for the simple algebra.





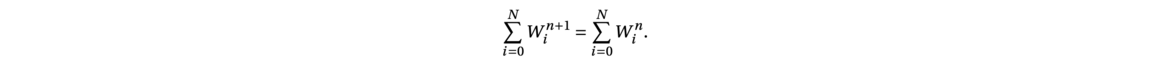
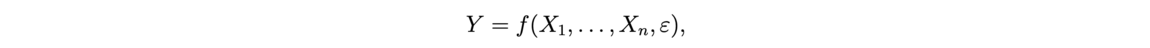
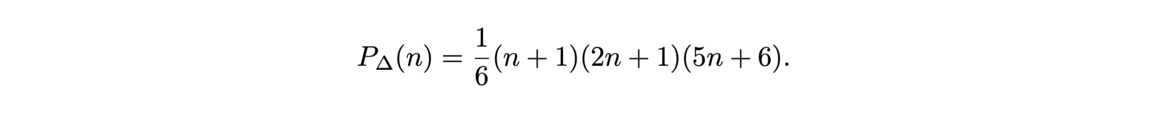
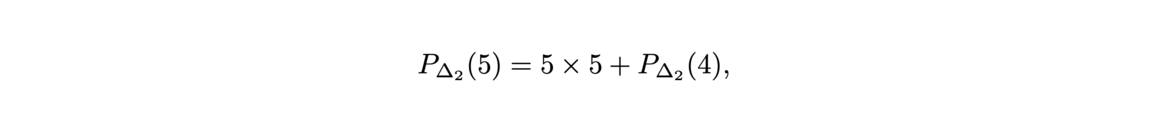
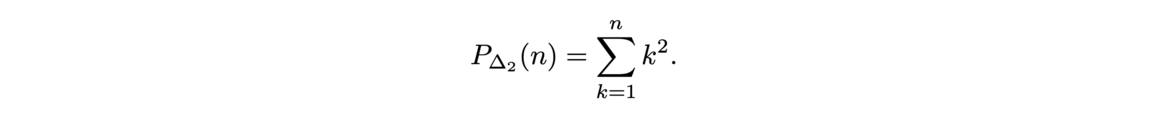
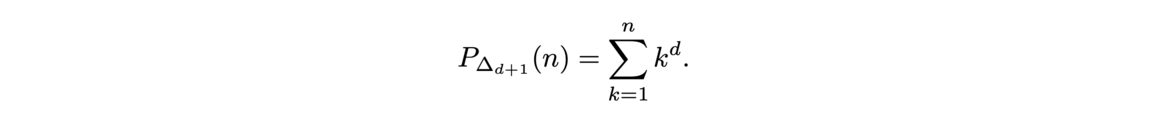

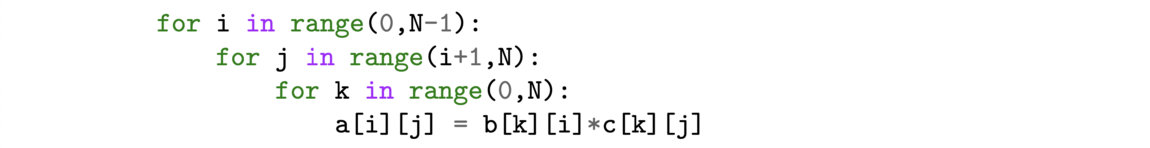
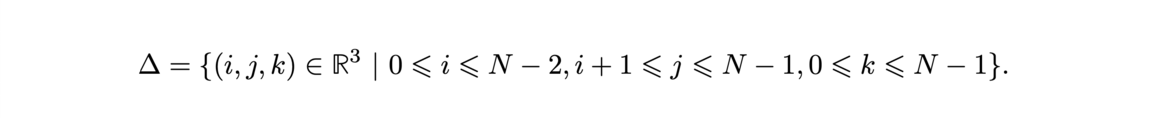

![Discrete-discrete (left) and discrete-continuous optimal transport (Source: [1]) Discrete-discrete (left) and discrete-continuous optimal transport (Source: [1])](/websites/_processed_/f/a/csm_f7-1_e7c31c89be.png)
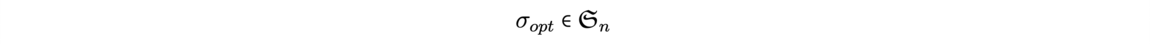
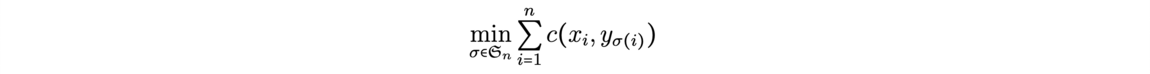
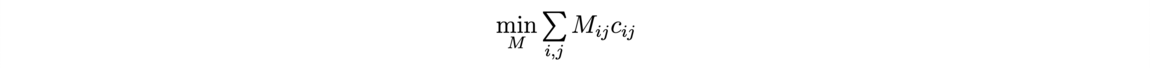
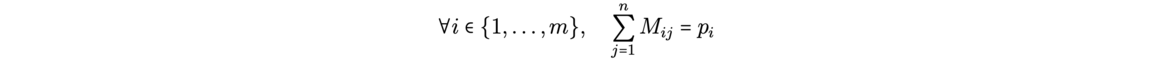
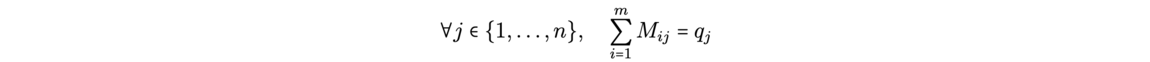
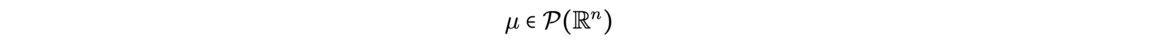
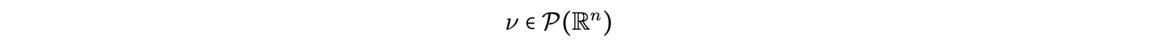
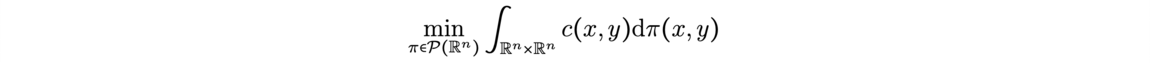
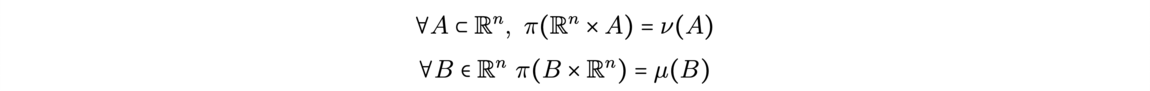
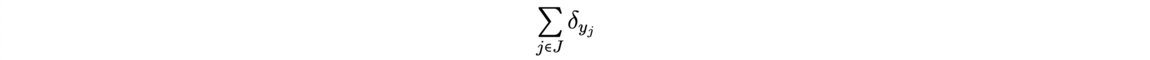
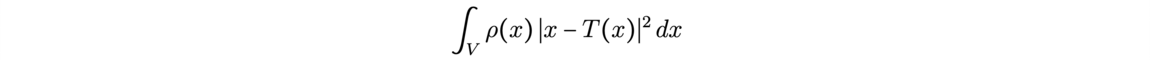
![Reconstruction of the initial cosmological density field (Source: [1]) Reconstruction of the initial cosmological density field (Source: [1])](/websites/ITI-IRMIApp/Journal-Etudiants-DU/f7-2.png)

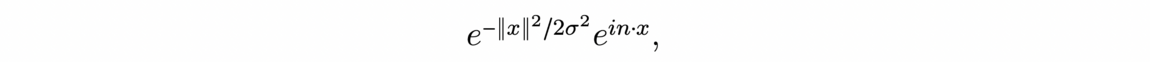
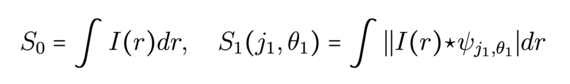
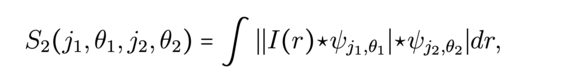
![Computation of Phase Harmonic Wavelet moments (Source: [1])](/websites/_processed_/f/8/csm_illu6-2_e285add756.png)
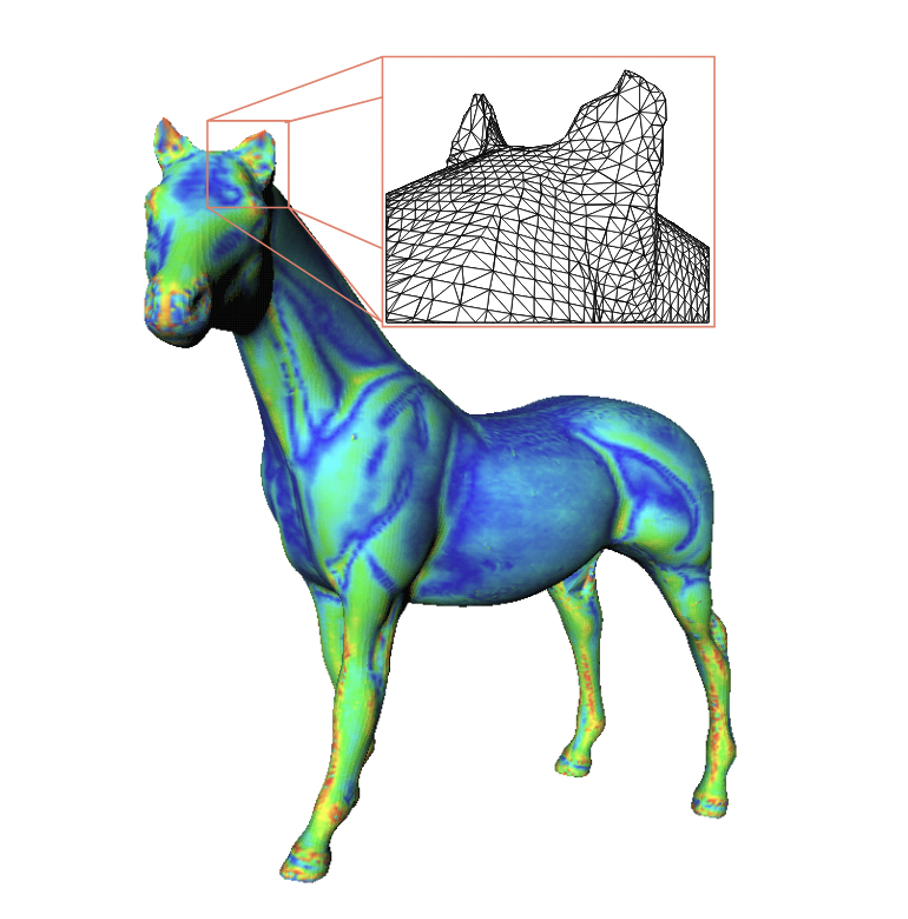
![A shape and its digitization (Source: [1])](/websites/ITI-IRMIApp/Journal-Etudiants-DU/illu5-1.png)
![Detection of edges in a cloud of points (Source: [2])](/websites/_processed_/b/2/csm_illu5-2_bd5915f01f.png)